ルワンダで教育支援を行うにあたり、改めて教育を受ける意義であったり、関連する支援活動を調べていて気付いたことが少しあります。
まず、貧困国においては上からの搾取を防ぐために教育は欠かせないものであり、また、支援活動で最も多いのは東南アジアでの学校建設でした。
 あやか
あやかここも、ここも学校を建設してる!こんなに学校を建てているのは日本人だけじゃないだろうし、よく飽和しないなぁ…。
学生の頃、建築学科やほかの大学の国際系学部の友人の何人かが学校建設プロジェクトに参加していて、ポスターもたまに見かけました。
こんなに何十年もアジアの学校建設をたくさんの団体がやってまだ足りてないだなんて、アフリカはもう尚さらじゃないか!って思ってしまいます。
しかし学習だけにフォーカスを当てると、学校じゃなくても勉強はできるんですよね。
もちろん私は「学校に行かなくていい」と言っているわけではなく、学校という小さな社会に加わること自体に価値があるのは十分わかっています。
.
.


でも、探究心や好奇心があれば、
人はどこでも勝手に学ぼうとするものでは?
私は数学が好きですが、数学ができる人は探究心と集中力がかなり強い傾向にあります。
たとえば、古代の数学者は、尽きない探究心を原動力にして、公式はおろか紙や計算機すらない時代に独自の解法を生み出し、ただ、シンプルな法則や規則を見つけて地道に一つの答えを導いたのです。
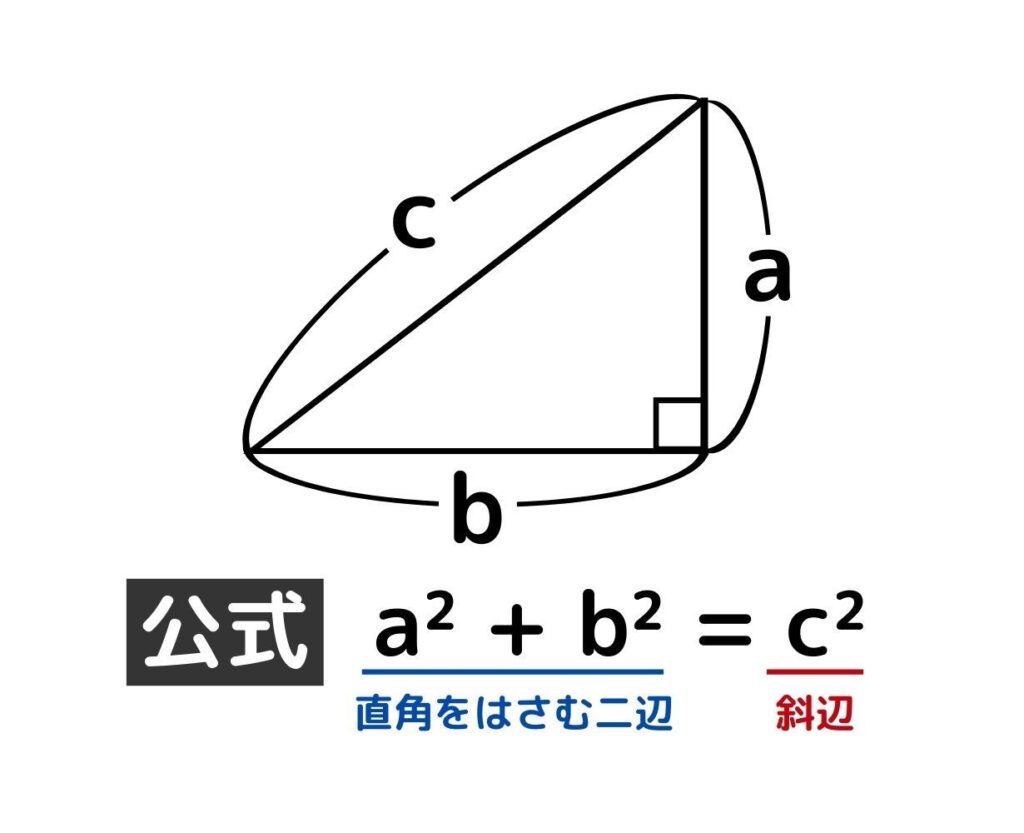

三平方の定理は古代ギリシアの数学者・哲学者ピタゴラスによって発見された。直角三角形の3辺の長さ a, b, c のうちの2つが分かれば、残り1辺の長さも求まる=2つの角度が分かれば距離が求まる。建築やものづくり、天文観測、ゲーム開発においても欠かせない定理である。
近年でも、高校中退&薬物中毒の殺人犯が刑務所での服役中に【連分数の超難問】を解いたとか、5人の子どもを持つごく平凡な主婦が子どもの勉強を見てあげているうちに【数学の未解決問題】を解いてしまったというニュースがありました。
こんな例を知ると、数学って案外どこでもやれる学問なんだと認めざるを得ません。
分かりやすい参考書さえあれば独学も決して不可能ではなく、学校で学んでいる子どもたちにとっても参考書は強い味方になるし、なにより数学を学ぶと自然に論理的思考能力を養うことができます。



だから、子どもから大人まで読めるような参考書を作りたい!
あと、どうやってアルキメデスが円周率を求めたかとか、床のタイルの模様から発見されたピタゴラスの定理とか、そういう小話も知るとさらに数学が面白く感じられるのでは?と思います。


アフリカ布の柄や編みカゴでも、まるで素数を意識したかのようなデザインがあったりして、アフリカンアートとフィボナッチ数列を掛け合わせたらさらに魅力的な作品ができるかも…。
なんて考えてしまう私はちょっとアレかもしれませんが、数学はアートに通じるところもあります。
アフリカには記号や曲線を描くようなアートがとても多くて、これを美しいと感じるのは本能であり、作者が意識せずとも黄金比や幾何学など数学的要素が散りばめられているのは感慨深い!
巷では言語学習が依然として流行っていて、そちらに力を入れる人も多いと思います。
でも、数学は計算力や論理的思考力が身につくだけじゃなくて、ふだんの生活の場からものづくりにも応用が効くし、分かりやすい説明ができる人は数学ができる人だという統計まであったりします。
この支援事業に関心を持ってくださっている方にお伝えしますが、まずは初等教育向けの算数の参考書を作りたいと思っているので、数学アレルギーであっても身構えないでください。
むしろ、皆さんと算数の問題を考えることで一緒に学んでいけるような、お互いにとって利点のある教育支援になるのではないか?と思っています。








コメント